PV = L * (1 - (1 + r) -n / r)
Hvori,- PV er nutidsværdien af udestående balance
- L er den eksisterende betaling
- r er rentesatsen
- n er hyppigheden af betalinger
Lommeregner til gæld
Gældsudbetalingsberegner er en type regnemaskine, hvor hvis låntager ønsker at konsolidere de udestående lån og forsøge at betale dem hurtigt for at reducere rentebyrden og det overskydende beløb.
Om gældsudbetalingsberegner
Find først ud af nutidsværdien af de udestående saldi på de flere lån.
PV = L * (1 - (1 + i) -n / r)Dernæst ville det være at finde ud af det nye raterbeløb, som enten kunne være summen af det eksisterende raterbeløb og yderligere betaling, hvis der skulle foretages nogen.
Beregn nu den periode, inden for hvilken gælden kan afbetales
nPVA = ln ((1 - PV (i) / L ') -1) ) / ln (1 + i)Hvori,
- PV er nutidsværdien af udestående balance
- L er den eksisterende betaling
- L 'er den nye betaling
- jeg er rentesatsen
- n er hyppigheden af betalinger
- nPVA er antallet af periodiske betalinger
Det er en praktisk lommeregner, da den beregner, hvad der vil være ansættelsesperioden, når al gæld er betalt. I dette tilfælde kan låntager sidde med flere lån med forskellige rentesatser og er villig til at konsolidere dem. Endvidere kunne låntager endda ønske at forhøje afdragsbeløbet med jævne mellemrum eller også konsolidere afdragsbeløbet. Dette skal hjælpe ham med at reducere rentebyrden og også afvikle gæld tidligt. Beslutningen er ikke så let som den krævede at øge afdragsbeløbet, hvilket kunne øge byrden for låntagerens pengestrøm. Denne lommeregner hjælper kun med at beregne inden for hvilket tidsrum de kan betale hele gælden, når gælden er konsolideret.
Sådan beregnes ved hjælp af gældsudbetalingsberegner?
Man er nødt til at følge nedenstående trin for at beregne den periode, hvor konsolideret gæld betaler sig.
Trin # 1 - For det første skal låntager bestemme, hvad der er den aktuelle gæld, der ikke er andet end at finde ud af gældens nuværende værdi.
Trin # 2 - Bestem nu det nye raterbeløb, som er summen af det eksisterende raterbeløb, som han i øjeblikket betaler, og det yderligere beløb, som låntager overvejer at starte med.
Trin # 3 - Find ud af lånet, som er højere rentebærende og klart, at gæld betaler sig først og fortsætter med at betale minimums- eller afdragsbeløb for andre udestående lån.
Trin # 4 - Beregn nu den udestående hovedstol på de resterende lån og beregne lånets løbetid med det nye afdragsbeløb.
Trin # 5 - Den resulterende ansættelse kan konverteres til år ved at dividere den værdi, der er ankommet i trin 4, med 12, og tal på højre side af decimalet kan ganges med 12 for at få dem i måneder.
Eksempel
Hr. X har to udestående lån, et er et automatisk lån, og et andet er et realkreditlån.
Oplysningerne om begge lån er angivet nedenfor:

Filialchefen har henvendt sig til Hr. X med en ordning, hvor han kan konsolidere de udestående lån og kan betale gæld tidligt. Bankmanden gav ham skemaoplysninger, der skulle betale den højere gæld først og derefter fortsætte det faste beløb på det lukkede lån, der skulle tilbagebetales på realkreditlånet, hvilket reducerer hans ansættelse af lånelukning. Hr. X indvilligede også i at hæve afdragsbeløbet med $ 200, mens han konsoliderede de udestående lån, og vil fortsætte med at gøre det, indtil gælden er afbetalt.
Det kræves, at du beregner den tid, som gælden skal betales af.
Løsning:
Vi skal beregne nutidsværdien af den aktuelle udestående gældsbalance, som kan beregnes i henhold til nedenstående formel:
Autolån
Rente gældende på månedsbasis = 8/12 = 0,67%
Den resterende periode vil være (7 * 12) - (3 * 12), som er 84 - 36, det vil sige 48.
PV = L * (1 - (1 + i) -n / r)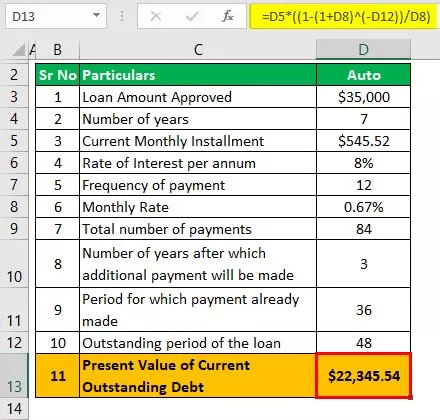
- = $ 545. 52 * (1 - (1 + 0,67%) -48 ) / 0,67%)
- = $ 22.345,54
Realkreditlån
Rente gældende på månedsbasis = 5/12 = 0,42%
Den resterende periode vil være (25 * 12) - (10 * 12), hvilket er 300 - 120, dvs. 180.
PV = L * (1 - (1 + i) -n / r)
- = $ 1.227,64 * (1 - (1 + 0,42%) -180 / 0,42%)
- = $ 155.241,51
Konsolideret udestående lån

- = $ 22.345,44 + $ 155.241,40
- = $ 177.586,84
Vi får her, den eksisterende månedlige rate, som han betaler på et autolån, er $ 545,52, og det nuværende raterbeløb på et realkreditlån er $ 1.227,64. Konsolideret afdragsbeløb ville være $ 1.773,16, og yderligere vil X også øge dette beløb med $ 200. Derfor vil det samlede nye raterbeløb være $ 1.973,16
For det første ville afdragsbeløbet på det automatiske lån blive afbetalt siden dets højere rentebærende, og det nye beløb, der ville blive brugt til at betale auto-lånet, ville være $ 545,52 + $ 200, hvilket er $ 745,52, og hvilebeløbet vil blive brugt til at betale ud af realkreditlån, der er $ 1.973,16 - $ 745,52, der svarer til $ 1,227,64
Nu skal vi beregne inden for hvilket tidsrum, der vil blive ryddet af autolån
nPVA = ln ((1 - PV (i) / L ') -1) ) / ln (1 + i)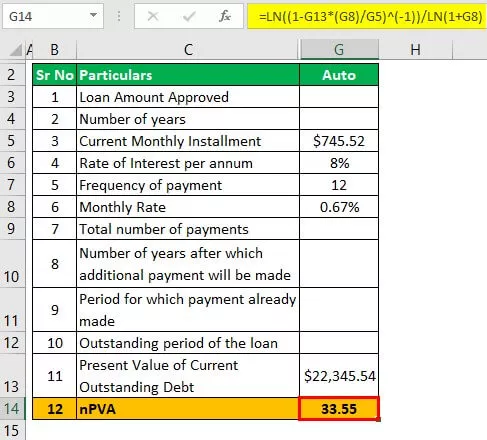
- = ln (((1- 22,345.44 * (0,67%) / 745,52) -1 ) / ln (1 + 0,67%)
- = 33,55
Nu vil udestående fast ejendomslån være 180 minus 33,55, hvilket er 146,45
Pantelån efter automatisk lån er betalt
Rente gældende på månedsbasis = 5/12 = 0,42%
PV = L * (1 - (1 + i) -n / r)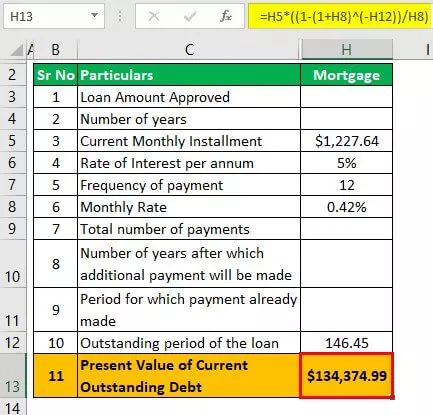
- = $ 1.227,64 * (1 - (1 + 0,42%) -146,45 / 0,42%)
- = $ 134.374,99
Nu skal vi beregne inden for hvilket tidsrum, der vil blive ryddet af realkreditlån
nPVA = ln ((1 - PV (i) / L ') -1 ) / ln (1 + i)
- = ln (((1- 134,374.92 * (0,42%) / 1,973,16) -1 ) / ln (1 + 0,42%)
- = 80,26
Derfor er den samlede tid, inden for hvilken lånet kan ryddes, 33,55 + 80,26, hvilket er 113,81, og når det samme divideres med 12, hvilket er 9,48 år, dvs. 9 år og 6 måneder.








