Sammensat definition
Sammensætning er metoden til beregning af rentesats, der rent faktisk er renter på renter, hvor renter beregnes af investering / initial hovedstol plus optjent rente og andre reinvesteringer, med andre ord akkumuleres rente til hovedstol afhængigt af tidsperioden for indskud eller lån det kan være månedligt, kvartalsvis eller årligt
Lad os prøve at forstå, hvad der sammensættes, og hvordan det fungerer gennem nogle grundlæggende eksempler
Top 4 eksempler på sammensætning
Eksempel nr. 1
Shane og Mark besluttede begge at investere $ 1.00.000, men Shane besluttede at investere i simpel rente, mens Mark investerer i sammensat rente i ti år til 10% rente. Lad os se, hvad der sker efter ti år.
Løsning:
Så beregningen af Shane-investering vil være -

Samlet indtjeningsbeløb = $ 200.000
Med en simpel interesse får Shane $ 2.00.000 efter 10 år.
Beregningen af varemærkeinvestering vil være -

Samlet indtjeningsbeløb = $ 2.59.374
Med sammensatte renter vil Marks investeringsværdier vokse til $ 2.59.374.
Nu besluttede Shane at investere gennem sammensatte metoder som Mark, og de investerede begge $ 2.00.000 til en sats på 15%.
Beregningen af Shane-investering vil være -

Samlet indtjeningsbeløb = $ 8,09,111,55
Shane forbliver investeret i 10 år og får det endelige beløb som $ 8,09,111,55 med en sats på 15%.
Beregningen af varemærkeinvestering vil være -

Samlet indtjeningsbeløb = $ 65,83,790.52
Mark er imidlertid tålmodige langsigtede investorer og forbliver investeret i 25 år, og hans investeringsværdi vokser til $ 65,83,790,52
Ovenstående eksempel viser sammensætningen. Jo længere investeringshorisonten er, desto større er den eksponentielle vækst.
Eksempel nr. 2 (ugentligt)
Simon har $ 7500 i besparelser, og for sin søns collegefond, der skal gå på kollegiet efter 15 år, besluttede han at investere i amerikanske sparebonds. Simons mål er at spare $ 20.000, og den årlige procentsats for en amerikansk opsparingsobligation er 6%. Hvad er den fremtidige værdi af Simon Money efter 15 år?
Løsning:
Givet,
- Principal = $ 7500
- Sats = 6% eller 0,06
- Tidsperiode = 15 år.
- Hvor mange gange er det sammensat på et år n = 52 uger
- Fremtidig værdi =?
Så beregningen af fremtidig værdi vil være -

Formlen for ugentlig sammensætning er som nedenfor.
F = P (1 + r / n) n * t- F = $ 7500 (1 + 0,06 / 52) 52 * 15
- F = $ 7500 (1 + 0,001153846) 780
- F = $ 18.437,45
Så fra ovenstående beregning er det klart, at Simons mål om at spare $ 20,00 ikke opnås med ovenstående metoder, men det er tættere på det.
Kontinuerlig sammensætningsmetode
Lad os nu prøve ovenstående eksempel med Continuous Compounding Formula.
Så beregningen af fremtidig værdi vil være -

- F = $ 7500e 0,06 * 15
- F = $ 7500e 0,9
- Fremtidig værdi (F) = $ 18.447,02
Selv med kontinuerlig sammensætning kan Simons mål om at spare 20.000 dollars til sin søns universitetsfond ikke nås.
Lad os se med månedlig sammensat formel, at hvor mange penge havde Simon brug for at investere for at nå sit mål om at spare $ 20.000 på 15 år med en APR på 6%?
Så beregningen af fremtidig værdi vil være -
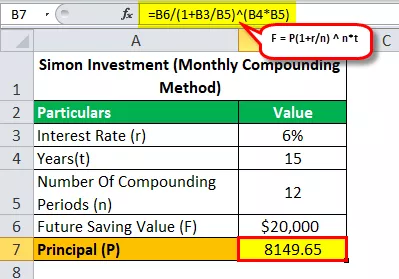
- $ 20.000 = P (1 + 0.06 / 12) 12 * 15
- P = $ 20.000 / (1 + 0.06 / 12) 12 * 15
- Opdragsgiver (P) = 8149,65
Så ved at løse ovenstående ligning får vi et svar, der er $ 8.149,65 (Beløb, som Simon skal investere for at nå sit mål om at spare $ 20.000 på 15 år).
Eksempel # 3 (Effektiv årlig udbytte)
Lad os sige XYZ-begrænset bank giver 10% om året til ældre borgere for fast indskud, og vi antager her, at bankinteressen kvartalsvis er sammensat som alle andre banker. Beregn det effektive årlige udbytte i 5, 7 og 10 år.
Løsning:
Årlig afkast i 5 år:
- t = 5 år
- n = 4 (kvartalsvis sammensat)
- I = 10% om året
Så A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 om 5 år
Effektiv interesse = 0,6386 / 5
Effektiv I = 12,772% pr. År
Årlig udbytte i 7 år:
- t = 7 år
- n = 4 (kvartalsvis sammensat)
- I = 10% om året
Så A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1.9965 om 7 år
- Effektiv I = 0,9965 / 7
Effektiv I = 14,236% pr. År
Årlig afkast i 10 år:
- t = 10 år
- n = 4 (kvartalsvis sammensat)
- I = 10% om året
Så A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1.685 om 10 år
- Effektiv I = 1.685/10
Effektiv I = 16,85% pr. År
Eksempel # 4 - (Annuiteter: Fremtidig værdi)
Der investeres $ 1.000 hver 3. måned til 4,8% om året sammensat kvartalsvis. Hvor meget vil livrenten være værd på 10 år?
Løsning:
Så når vi siger, hvor meget livrenten vil være værd om 10 år, betyder det, at vi her skal finde fremtidig værdi, og dette er vigtigt, for når der er et eksempel på livrenter, skal vi se, hvad vi skal finde ud af.
Så formlen for fremtidig værdi er
FV af livrente = P ((1+ r) n - 1 / r)- P = Periodisk betaling
- r = sats pr. periode
- n = Antal perioder
Så formlen for fremtidig værdi er
- Så her er P = $ 1.000
- r = 4,8% pr. år eller 0,048
- r (kvartalsvis) = 0,048 / 4
- r (kvartalsvis) = 0,012
- n = 10 år
- n (Antal gange sammensætning vil gælde) = 10 × 4 = 40
Så beregningen af FV af livrente vil være -

Så nu FV = $ 1000 (1 + 0,012) 40 -1 / 0,012)
Så ved at løse ovenstående ligning får du en FV på $ 50.955,30
Så hvor meget er annuiteten om 10 år, og svaret er $ 50.955,30
Derudover kan vi også finde ud af ovenstående eksempel, hvor meget interesse der optjenes på 10 år.
Som 40 gange er der investeret $ 1000, dvs. en samlet investering (40 × $ 1000 = $ 40.000).
Så interesse = fremtidig værdi - samlet investering
- Rente = $ 50.955,30 - $ 40.000
- Rente = $ 10.955,30
Så her er det vigtigt at forstå, at i livrenter kan investorer tjene en masse interesse. I ovenstående særlige eksempler giver et depositum på $ 40.000 til gengæld en samlet rente på $ 10.955,30.
Bemærk: Du kan downloade den ovenstående Excel-skabelon til detaljeret beregning.








