Formel til beregning af annuitetsbetaling
Udtrykket "annuitet" henviser til den række periodiske betalinger, der skal modtages enten i begyndelsen af hver periode eller ved slutningen af perioden i fremtiden. Formlen for livrenteudbetaling og forfalden livrente beregnes på baggrund af solvens af en forfalden livrente, effektiv rente og et antal perioder.
Formlen, der er baseret på en almindelig livrente, beregnes på basis af solvensrente med en almindelig livrente, effektiv rente og flere perioder.
Annuitet = r * PVA Almindelig / (1 - (1 + r) -n )hvor,
- PVA Ordinary = nutidsværdien af en almindelig livrente
- r = Effektiv rente
- n = Antal perioder
Matematisk er ligningen for forfalden livrente repræsenteret som,
Annuitet = r * PVA Due / ((1 - (1 + r) -n ) * (1 + r))hvor,
- PVA Due = nutidsværdien af en forfalden livrente
- r = Effektiv rente
- n = antal perioder

Hvordan beregnes livrente? (Trin for trin)
Beregningen af annuitetsbetaling kan udledes ved hjælp af PV for almindelig livrente i følgende trin:
- Trin 1 : For det første skal du bestemme livrentens solvens og bekræfte, at betalingen vil ske i slutningen af hver periode. Det er betegnet med PVA Ordinary .
- Trin 2: Bestem derefter renten baseret på det aktuelle markedsafkast. Derefter beregnes den effektive rente ved at dividere den årlige rente med antallet af periodiske betalinger i et år, og den betegnes med r. r = årlig rente / antal regelmæssige betalinger om et år
- Trin 3: Bestem derefter antallet af perioder ved at multiplicere antallet af periodiske betalinger i et år og antallet af år, og det betegnes med n. n = antal regelmæssige betalinger i et år * Antal år
- Trin 4: Endelig beregnes livrentebetalingen baseret på solvens af en almindelig livrente baseret på solvensrenten af almindelig livrente (trin 1), effektiv rente (trin 2) og nogle perioder (trin 3) som vist ovenfor.
Beregningen af livrentebetaling kan også udledes ved hjælp af PV for en annuitet, der skal betales i følgende trin:
- Trin 1: For det første skal du bestemme livrentens PV og bekræfte, at betalingen vil ske i begyndelsen af hver periode. Det er betegnet med PVA Due .
- Trin 2: Bestem derefter renten baseret på det aktuelle markedsafkast. Derefter beregnes den effektive rente ved at dividere den årlige rente med antallet af periodiske betalinger i et år, og den betegnes med r. r = årlig rente / antal regelmæssige betalinger om et år
- Trin 3: Bestem derefter antallet af perioder ved at multiplicere antallet af periodiske betalinger i et år og antallet af år, og det betegnes med n. n = antal regelmæssige betalinger i et år * Antal år
- Trin 4: Endelig beregnes livrentebetalingen baseret på solceller af en forfalden livrente baseret på solvens af en annuitet (trin 1), effektiv rente (trin 2) og flere perioder (trin 3) som vist ovenfor.
Eksempler
Eksempel nr. 1
Lad os tage eksemplet med David, der vandt et lotteri til en værdi af $ 10.000.000. Han har valgt en annuitetsbetaling ved udgangen af hvert år i de næste 20 år som en udbetalingsmulighed. Bestem det beløb, som David vil blive betalt som annuitet, hvis den konstante rente på markedet er 5%.
Nedenfor er de data, der anvendes til beregning af livrenteudbetalinger.
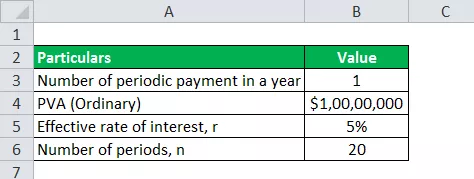
Almindelig PVA = $ 10.000.000 (siden livrenten skal betales ved udgangen af hvert år)
Derfor kan beregningen af udbetaling af livrente foretages som følger -
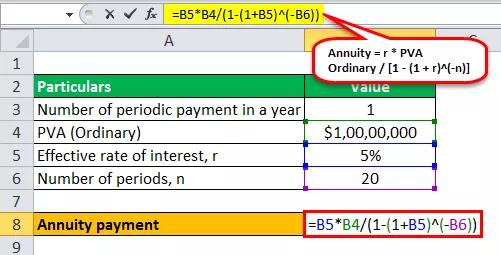
- Annuitet = 5% * $ 10.000.000 / (1 - (1 + 5%) -20 )
Beregning af annuitetsbetaling vil være -

- Annuitet = $ 802.425,87 ~ $ 802.426
Derfor betaler David annuitet på 802.426 $ i de næste 20 år i tilfælde af almindelig livrente.
Eksempel 2
Lad os tage ovenstående eksempel på David og bestemme livrenteudbetalingen, hvis den betales i begyndelsen af hvert år med alle andre betingelser det samme.
Vi bruger de samme data som ovenstående eksempel til beregning af annuitetsbetalinger.
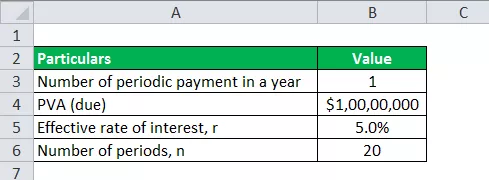
Derfor kan beregningen af udbetaling af livrente foretages som følger -
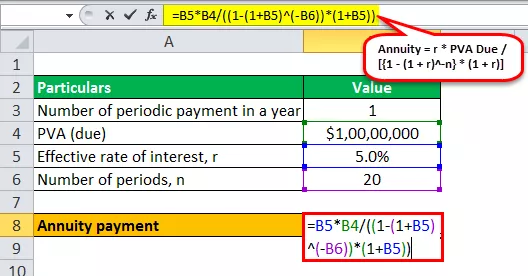
- Annuitet = r * PVA Due / ((1 - (1 + r) -n ) * (1 + r))
- Annuitet = 5% * $ 10.000.000 / ((1 - (1 + 5%) -20 ) * (1 + 5%))
Beregning af annuitetsbetaling vil være -
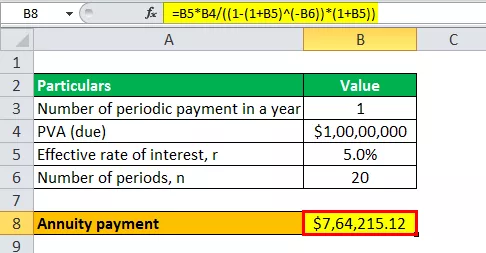
- Annuitet = $ 764,215.12 ~ $ 764,215
Derfor betaler David livrente på $ 764.215 i de næste 20 år i tilfælde af forfalden livrente.
Annuitetsberegner
Du kan bruge følgende annuitetsberegner.
| PVA Almindelig | |
| r | |
| n | |
| Annuitetsformel = | |
| Annuitetsformel = | r * |
|
||||||||
| 0 * |
|
Relevans og anvendelser
Livrenteudbetalingen er en af anvendelserne af pengernes tidsværdi, hvilket yderligere er angivet ved forskellen mellem annuitetbetalinger baseret på almindelig livrente og forfalden livrente. Den lavere livrente for en livrente er, at pengene modtages i starten af hver periode. Det antages, at midlerne vil blive investeret i markedet, og der vil blive optjent renter i denne periode.
Ligningen for annuitetsbetaling finder anvendelse ved beregning af indkomstrente, amortiserede lån, lotteriudbetalinger, strukturerede afregninger og enhver anden form for faste periodiske betalinger.








